DGL 1.0: Empowering Graph Machine Learning for Everyone

We are thrilled to announce the arrival of DGL 1.0, a cutting-edge machine learning framework for deep learning on graphs. Over the past three years, there has been growing interest from both academia and industry in this technology. Our framework has received requests from various scenarios, from academic research on state-of-the-art models to industrial demands for scaling Graph Neural Network (GNN) solutions to large, real-world problems. With DGL 1.0, we aim to provide a comprehensive and user-friendly solution for all users to take advantage of graph machine learning.

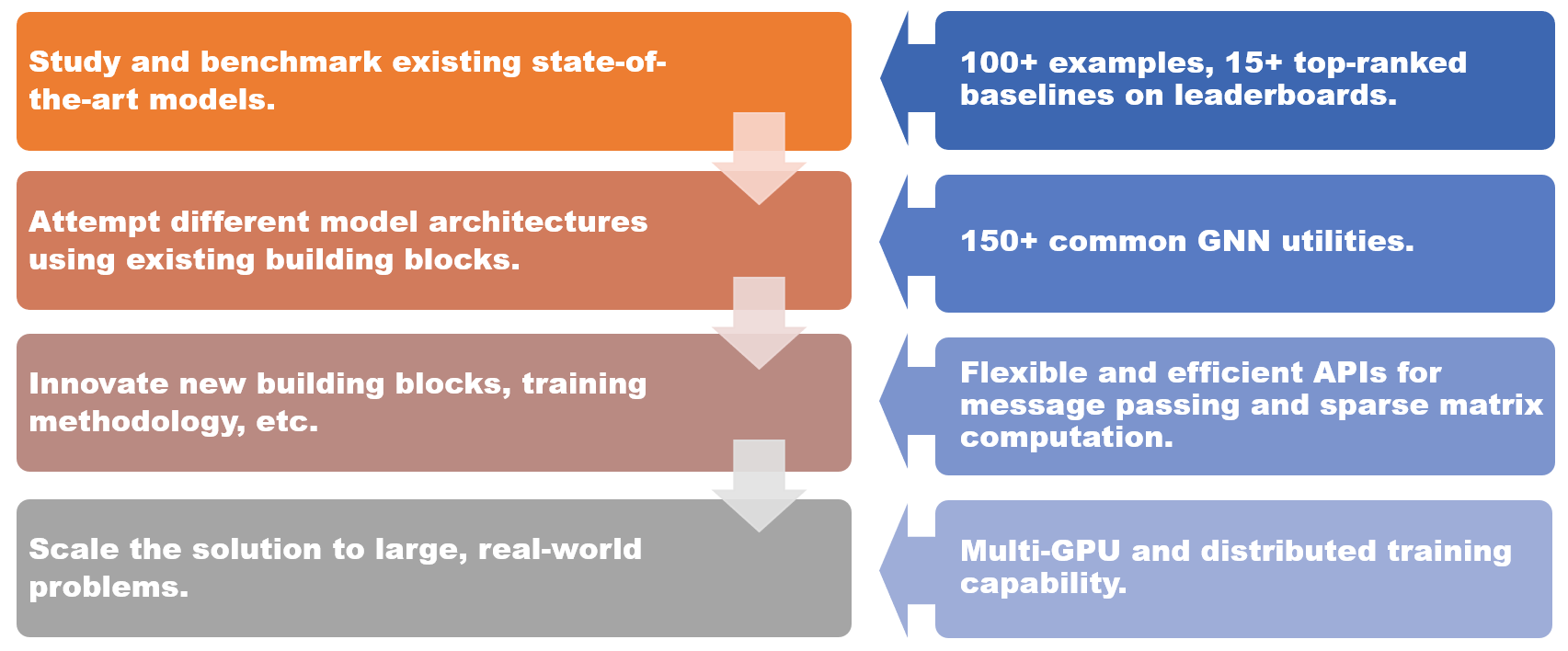
DGL 1.0 adopts a layered and modular design to fulfill various user requests. The key features of DGL 1.0 include:

• 100+ examples of state-of-the-art GNN models, 15+ top-ranked baselines on Open Graph Benchmark (OGB), available for learning and integration
• 150+ GNN utilities including GNN layers, datasets, graph data transform modules, graph samplers, etc. for building new model architectures or GNN-based solutions
• Flexible and efficient message passing and sparse matrix abstraction for developing new GNN building blocks
• Multi-GPU and distributed training capability to scale to graphs of billions of nodes and edges

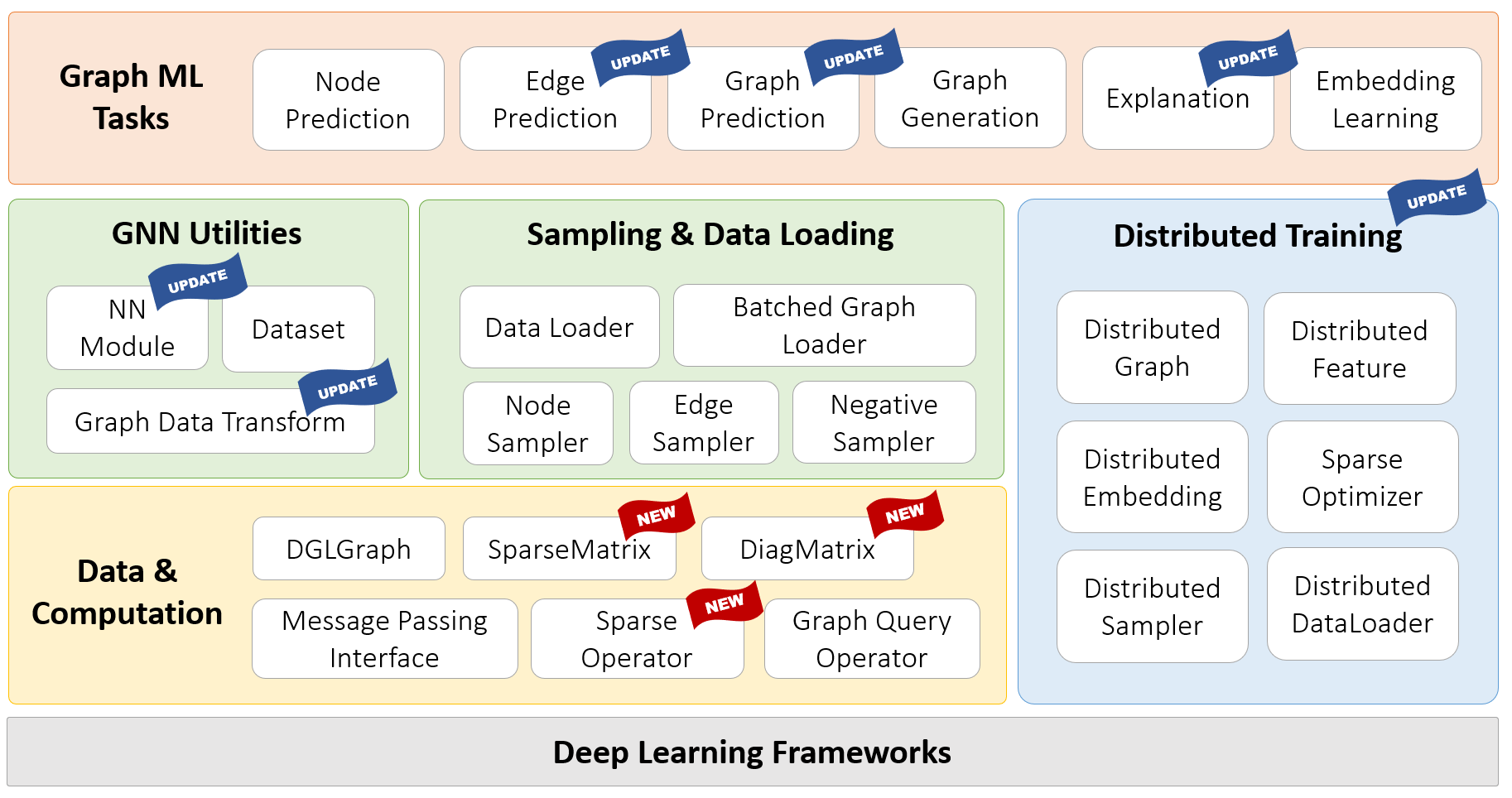
The new additions and updates in DGL 1.0 are depicted in the accompanying figure. One of the highlights of this release is the introduction of DGL-Sparse, a new specialized package for graph ML models defined in sparse matrix notations. DGL-Sparse streamlines the programming process not just for well-established GNNs such as Graph Convolutional Networks, but also for the latest models, including diffusion-based GNNs, hypergraph neural networks, and Graph Transformers. In the following article, we will provide an overview of two popular paradigms for expressing GNNs, i.e., the message passing view and the matrix view, which motivated the creation of DGL-Sparse. We will then show you how to get started with this new and exciting feature.

The Message Passing View v.s. The Matrix View

“It’s the theory that the language you speak determines how you think and affects how you see everything.” — Louise Banks from Film Arrival

Representing a Graph Neural Network can take two distinct forms. The first, known as the message passing view, approaches GNN models from a fine-grained, local perspective, detailing how messages are exchanged along edges and how node states are updated accordingly. Alternatively, due to the algebraic equivalence of a graph to a sparse adjacency matrix, many researchers opt to express their GNN models from a coarse-grained, global perspective, emphasizing the operations involving the sparse adjacency matrix and dense feature tensors.

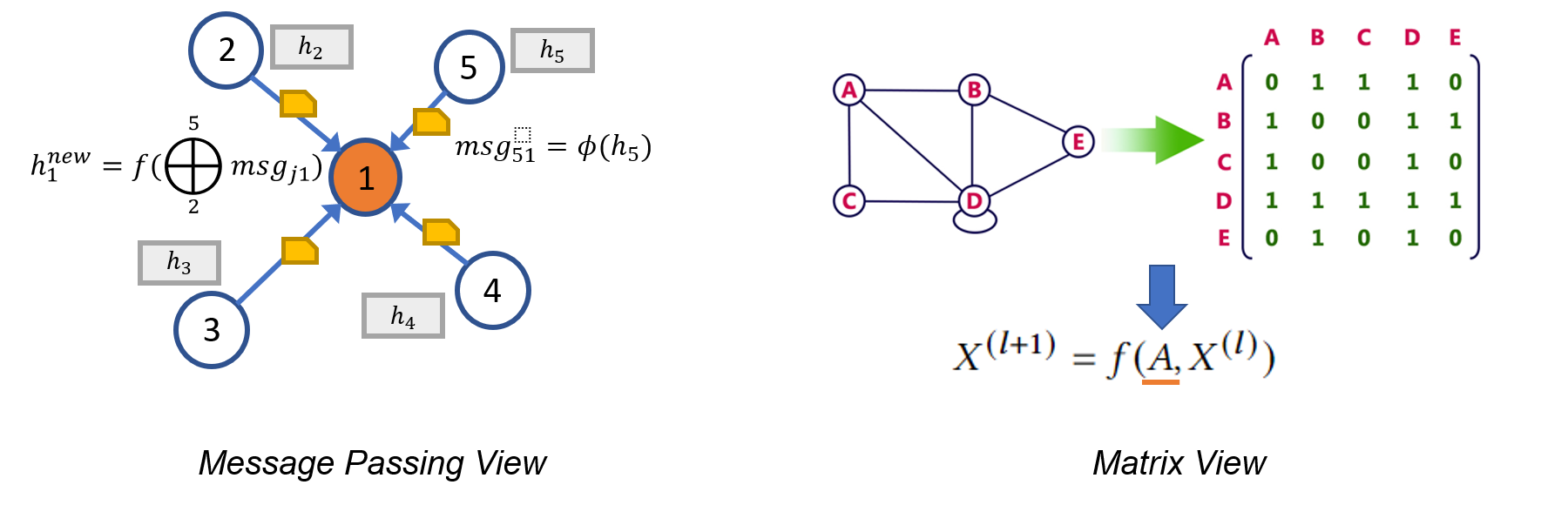
These local and global perspectives are sometimes interchangeable, but more often, provide complementary insights into the fundamentals and limitations of GNNs. For instance, the message passing view highlights the connection between GNNs and the Weisfeiler Lehman (WL) graph isomorphism test, which also relies on aggregating information from neighbors (as described in Xu et al., 2018). Meanwhile, the matrix view provides valuable understanding of the algebraic properties of GNNs, leading to intriguing findings such as the oversmoothing phenomenon (as discussed in Li et al., 2018). In conclusion, both the message passing view and matrix view are indispensable tools in studying and describing GNNs, and this is precisely what motivates the key feature we will be showcasing in DGL 1.0.

DGL Sparse: Sparse Matrix Abstraction for Graph ML

In DGL 1.0, we are happy to announce the release of DGL Sparse, a new sub-package (dgl.sparse) in addition to the existing message passing interface in DGL to accomplish the support of the entire spectrum of GNN models. DGL Sparse provides sparse matrix classes and operations specialized for Graph ML, making it easier to program GNNs described in the matrix view. In the following section, we will demonstrate a few examples of GNNs, showcasing their mathematical formulation and corresponding code implementation in DGL Sparse.

The Graph Convolutional Network (Kipf et al., 2017) is one of the pioneer works in GNN modeling. GCN can be expressed in both message passing view and matrix view. The code below compares the two different perspectives and implementations in DGL.

import dgl.function as fn  # DGL message passing functions

class GCNLayer(nn.Module):
    ...
    
    def forward(self, g, X):
        g.ndata['X'] = X
        g.ndata['deg'] = g.in_degrees().float()
        g.update_all(self.message, fn.sum('m', 'X_neigh'))
        X_neigh = g.ndata['X_neigh']
        return F.relu(self.W(X_neigh))
    
    def message(self, edges):
        c_ij = (edges.src['deg'] * edges.dst['deg']) ** -0.5
        return {'m' : edges.src['X'] * c_ij}

import dgl.sparse as dglsp  # DGL 1.0 sparse matrix package

class GCNLayer(nn.Module):
    ...
    
    def forward(self, A, X):
        D_invsqrt = dglsp.diag(A.sum(1)) ** -0.5
        A_norm = D_invsqrt @ A @ D_invsqrt
        return F.relu(self.W(A_norm @ X))

Graph Diffusion-based GNNs. Graph diffusion is a process of propagating or smoothing node features/signals along edges. Many classical graph algorithms such as PageRank belong to this category. A series of research has shown that combining graph diffusion with neural networks is an effective and efficient way to enhance model predictions. The equation below describe the core computation of one representative model — Approximated Personalized Propagation of Neural Prediction (Gasteiger et al., 2018), which can be implemented in DGL Sparse straightforwardly.

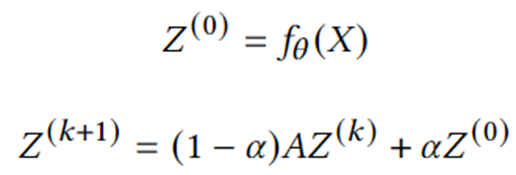
class APPNP(nn.Module):
    ...

    def forward(self, A, X):
        Z_0 = Z = self.f_theta(X)
        for _ in range(self.num_hops):
            A_drop = dglsp.val_like(A, self.A_dropout(A.val))
            Z = (1 - self.alpha) * A_drop @ Z + self.alpha * Z_0
        return Z

Hypergraph Neural Networks. A hypergraph is a generalization of a graph in which an edge can join any number of nodes (called an hyperedge). Hypergraphs are particularly useful in scenarios that require capturing high-order relations such as co-purchase behaviors in e-commerce platforms, or co-authorship in citation networks, etc. A hypergraph is typically characterized by its sparse incidence matrix, and thus Hypergraph Neural Networks (HGNN) are commonly defined in sparse matrix notations. The equation and code implementation of Hypergraph Convolution, proposed by Feng et al., 2018, are presented below.

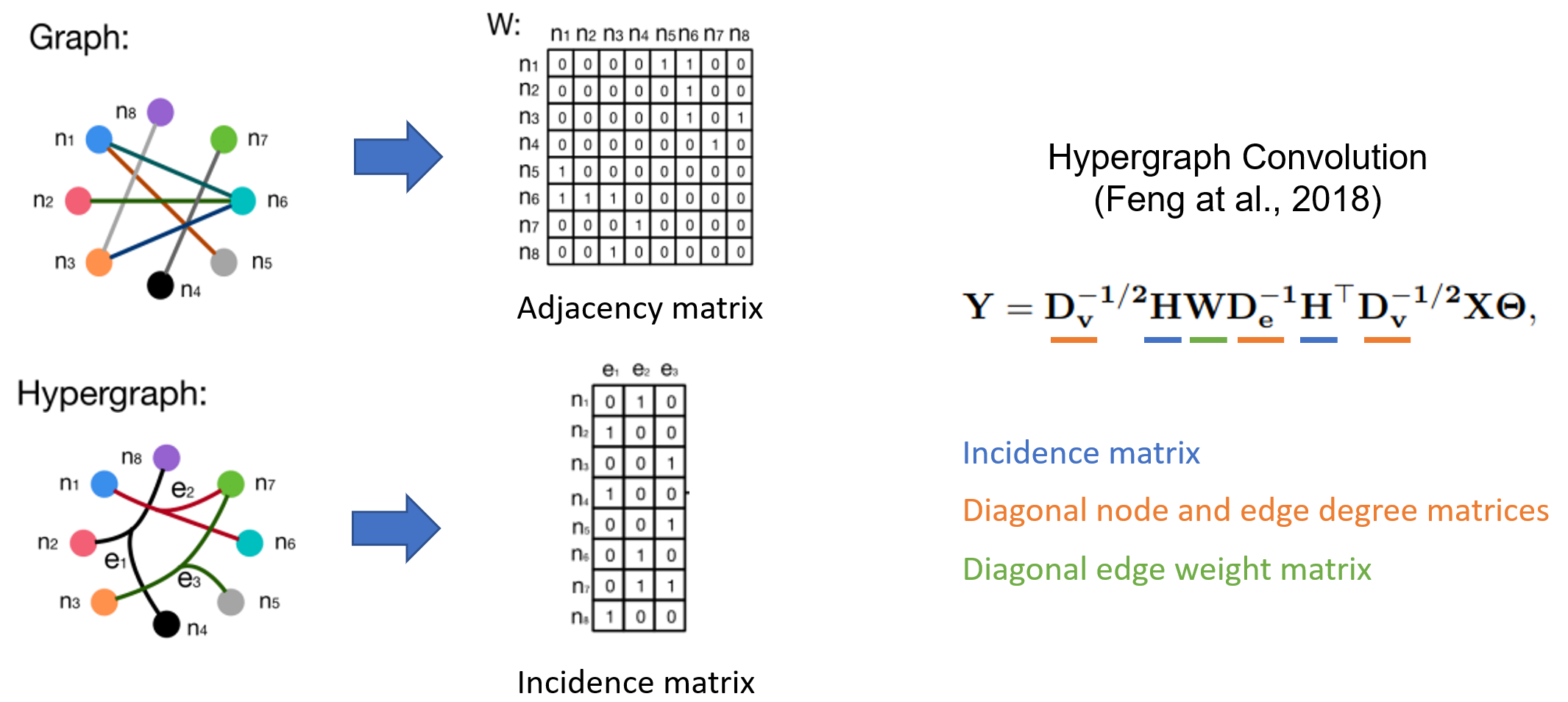
class HypergraphConv(nn.Module):
    ...

    def forward(self, H, X):
        d_V = H.sum(1)  # node degree
        d_E = H.sum(0)  # edge degree
        n_edges = d_E.shape[0]
        D_V_invsqrt = dglsp.diag(d_V**-0.5)  # D_V ** (-1/2)
        D_E_inv = dglsp.diag(d_E**-1)  # D_E ** (-1)
        W = dglsp.identity((n_edges, n_edges))
        L = D_V_invsqrt @ H @ W @ D_E_inv @ H.T @ D_V_invsqrt
        return self.Theta(L @ X)

Graph Transformers. The Transformer has proven to be an effective learning architecture in natural language processing and computer vision. Researchers have begun to extend the use of Transformers to graph learning as well. One of the pioneer work by (Dwivedi et al., 2020) proposed to constrain the all-pair multi-head attention to the connected node pairs in a graph. With DGL Sparse, implementing this new formulation is now a straightforward process, taking only about 10 lines of code.

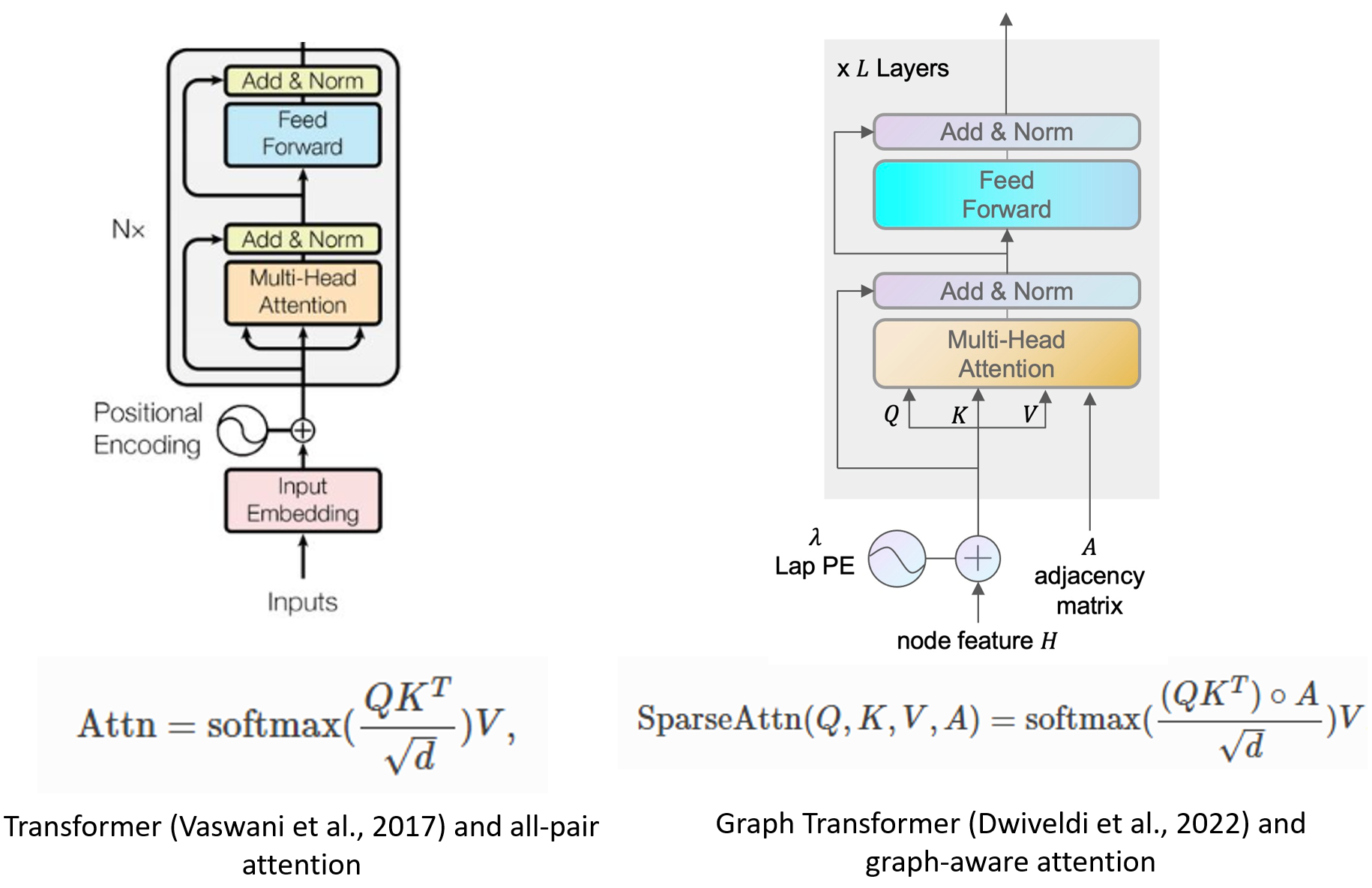
class GraphMHA(nn.Module):
    ...

    def forward(self, A, h):
        N = len(h)
        q = self.q_proj(h).reshape(N, self.head_dim, self.num_heads)
        q *= self.scaling
        k = self.k_proj(h).reshape(N, self.head_dim, self.num_heads)
        v = self.v_proj(h).reshape(N, self.head_dim, self.num_heads)

        attn = dglsp.bsddmm(A, q, k.transpose(1, 0))  # [N, N, nh]
        attn = attn.softmax()
        out = dglsp.bspmm(attn, v)

        return self.out_proj(out.reshape(N, -1))

Key Features of DGL Sparse

To handle diverse use cases in an efficient manner, DGL Sparse is designed with two key features that set it apart from other sparse matrix libraries such as scipy.sparse or torch.sparse:

• Automatic Sparse Format Selection. DGL Sparse eliminates the complexity of choosing the right data structure for storing a sparse matrix (also known as the sparse format). Users can create a sparse matrix with a single call to dgl.sparse.spmatrix and the internal DGL’s sparse matrix will automatically select the optimal format based on the intended operation.
• Scalar or Vector Non-zero Elements. GNN models often associate edges with multi-channel weight vectors, such as multi-head attention vectors, as demonstrated in the Graph Transformer example. To accommodate this, DGL Sparse allows non-zero elements to have vector shapes and extends common sparse operations, such as sparse-dense-matrix multiplication (SpMM), to operate on this new form (as seen in the bspmm operation in the Graph Transformer example).

By utilizing these design features, DGL Sparse reduces code length by 2.7 times on average when compared to previous implementations of matrix-view models with message passing interface. The simplified code also results in 43% less overhead in the framework. Additionally, DGL Sparse is PyTorch compatible, making it easy to integrate with the various tools and packages available within the PyTorch ecosystem.

Get started with DGL 1.0

The framework is readily available on all platforms and can be easily installed using pip or conda. To get started with DGL Sparse, check out the new Quickstart tutorial and play with it in Google Colab without having to set up a local environment. In addition to the examples you’ve seen above, the first release of DGL Sparse includes 5 tutorials and 11 end-to-end examples to help you learn and understand the different uses of this new package.

We welcome your feedback and are available via Github issues and Discuss posts. Join our Slack channel to stay updated and to connect with the community.

For more information on the new additions and changes in DGL 1.0, please refer to our release note.

(Banner image generated by Midjourney.)