Improving Graph Neural Networks via Network-in-network Architecture
As Graph Neural Networks (GNNs) has become increasingly popular, there is a wide interest of designing deeper GNN architecture. However, deep GNNs suffer from the oversmoothing issue where the learnt node representations quickly become indistinguishable with more layers. This blog features a simple yet effective technique to build a deep GNN without the concern of oversmoothing. The new architecture, Network in Graph Neural Networks (NGNN) inspired by the network-in-network architecture for computer vision, has shown superior performance on multiple Open Graph Benchmark (OGB) leaderboards.
Introducing NGNN
At a high-level, a graph neural network (MPGNN) layer can be written as a non-linear function:
with being the input node features, being the input graph, being the node embeddings in the last layer used by downstream tasks, being the number of GNN layers. Additionally, the function is determined by learnable parameters and is a non-linear activation function.
Instead of adding many more GNN layers, NGNN deepens a GNN model by inserting nonlinear feedforward neural network layer(s) within each GNN layer.
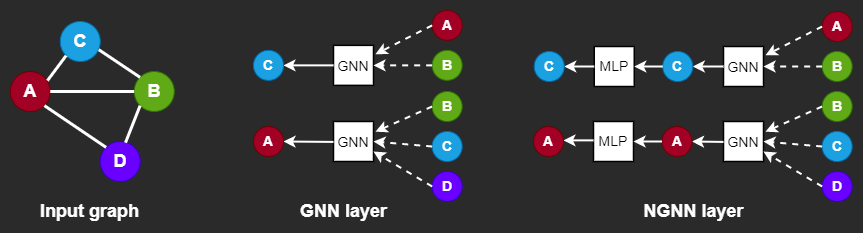
In essence, NGNN is just a nonlinear transformation of the original embeddings of the nodes in the -th layer. Despite its simplicity, the NGNN technique is quite powerful (we will come to that in a moment). Additionally, it does not have large memory overhead and can work with various training methods such as neighbor sampling or subgraph sampling.
The intuition behind is straightforward. As the number of GNN layers and the number of training iterations increases, the representations of nodes within the same connected component will tend to converge to the same value. NGNN uses a simple MLP after certain GNN layers to tackle the so-called oversmoothing issue.
Implementing NGNN in Deep Graph Library (DGL)
For better gaining insights into this trick, let us use DGL to implement a simple NGNN, using the GCN layer as the backbone.
With DGL’s builtin GCN layer dgl.nn.GraphConv, we can easily implement a
minimal NGNN_GCN layer, which just applies an activation and a
linear transformation after a GCN layer.
from dgl.nn import GraphConv
class NGNN_GCNConv(torch.nn.Module):
def __init__(self, input_channels, hidden_channels, output_channels):
super(NGNN_GCNConv, self).__init__()
self.conv = GraphConv(input_channels, hidden_channels)
self.fc = Linear(hidden_channels, output_channels)
def forward(self, g, x, edge_weight=None):
x = self.conv(g, x, edge_weight)
x = F.relu(x)
x = self.fc(x)
return x
Afterwards, you can simply stack the dgl.nn.GraphConv layer and the
NGNN_GCN layer to form a multi-layer NGNN_GCN network.
class NGNN_GCN(nn.Module):
def __init__(self, input_channels, hidden_channels, output_channels):
super(Model, self).__init__()
self.conv1 = NGNN_GCNConv(input_channels, hidden_channels, hidden_channels)
self.conv2 = GraphConv(hidden_channels, output_channels)
def forward(self, g, input_channels):
h = self.conv1(g, input_channels)
h = F.relu(h)
h = self.conv2(g, h)
return h
You can replace dgl.nn.GraphConv with any other graph convolution layers in
the NGNN architecture. DGL provides implementation of many popular
convolutional layers and utility modules. You can easily invoke them with one
line of code and build your own NGNN modules.
Model Performance
NGNN can be used for many downstream tasks, such as Node Classification/Regression, Edge Classification/Regression, Link prediction and Graph Classification. In general, NGNN achieves better results than its backbone GNN on these tasks. For instance, NGNN+SEAL achieves top-1 performance on the ogbl-ppa leaderboard with an improvement of Hit@100 by over the vanilla SEAL. The table below shows the performance improvement of NGNN over various vanilla GNN backbones.
| Dataset | Metric | Model | Performance | |
|---|---|---|---|---|
| ogbn-proteins | ROC-AUC(%) | GraphSage+Cluster Sampling | Vanilla | 67.45 ± 1.21 |
| +NGNN | 68.12 ± 0.96 | |||
| ogbn-products | Accuracy(%) | GraphSage | Vanilla | 78.27 ± 0.45 |
| +NGNN | 79.88 ± 0.34 | |||
| GAT+Neighbor Sampling | Vanilla | 79.23 ± 0.16 | ||
| +NGNN | 79.67 ± 0.09 | |||
| ogbl-collab | hit@50(%) | GCN | Vanilla | 49.52 ± 0.70 |
| +NGNN | 53.48 ± 0.40 | |||
| GraphSage | Vanilla | 51.66 ± 0.35 | ||
| +NGNN | 53.59 ± 0.56 | |||
| ogbl-ppa | hit@100(%) | SEAL-DGCNN | Vanilla | 48.80 ± 3.16 |
| +NGNN | 59.71 ± 2.45 | |||
| GCN | Vanilla | 18.67 ± 1.32 | ||
| +NGNN | 36.83 ± 0.99 |
Further Readings
- NGNN Paper: https://arxiv.org/abs/2111.11638
- NGNN+SEAL OGB submission: https://github.com/dmlc/dgl/tree/master/examples/pytorch/ogb/ngnn_seal
- NGNN+GraphSAGE OGB submission: https://github.com/dmlc/dgl/tree/master/examples/pytorch/ogb/ngnn
- DGL built-in GNN module list: https://docs.dgl.ai/api/python/nn-pytorch.html
About the author: Yakun Song is an undergraduate student of Shanghai Jiao Tong University. The work was done during his internship in AWS Shanghai AI Lab.
28 November
By Yakun Song, in blog

